Square of Nine 6.1 Converting Price and Time to Degress of a Circle

A Visualization of Spatial Relationships

Artistic representation – the numerical order, however, is not perfect.

Before moving ahead, let’s review the conceptual framework of what we have accomplished. We started everything with the description of the Square of Nine paper version. You can view the form of the paper version in Appendix 1 if you haven’t already done so. We created the visualization of how you can turn the two-dimensional Square of Nine table into a three-dimensional pyramid by grabbing the center of the table and pulling it straight up until all the sides are perfectly shaped into a pyramid.

Each block in the pyramid is a number in the table. This visualization enables us to see the spatial relationships between the numbers and how they relate to each other by angles and sides and position on the pyramid. When viewed looking down from directly above the numeral one at the apex of the pyramid we can see how the blocks can be stretched and pulled into the geometric shapes of a circle, a smaller triangle, and a square without losing their spatial relationships to each other.

A little heavy on the visualization? Maybe so, but before tackling the more esoteric applications of the Square of Nine, where both price and time are interchangeable to and from degrees of a circle, we want to reinforce an awareness that the axis boundaries and the price bars on our stock charts are really just the literal representations of the spatial relationship of price and time.

And finally, we can precisely determine the location of these spatial relationships, in some circumstances well into the future, by manipulating the square root of price and time’s position on the Square of Nine with the decimal equivalents of the divisions of a circle.

Price or Time Converted to Degrees – the Formula

The formula for converting a price level or a number of bars or calendar days to degrees of a circle is straightforward and can be done on any calculator with a square root function key or a power function key.

The formula for Excel is: MOD((SQRT( (N))*180)-225,360) where N is the price, or price range, or time in days or bars that we want to convert.

Punching the formula into a $10 calculator is more labor-intensive because of the MOD 360 business. Here’s the keystroke sequence for finding the degrees of circle for the number 74.

The only curveball is in Step 4, where you subtract 3 from 3.676. This step is necessary to accomplish the MOD 360 function, limiting the final answer to a number between 1 and 360. For this example with N=74, you subtracted 3, the whole number to the left of the decimal point, before multiplying by 360 in Step 5. If N=265, the whole number to the left of the decimal point would be 7, so you would subtract 7 from the intermediate result of Step 3, and so on.

The Excel table below shows the precompiled degrees for all the numerals between 1 and 225. The Excel formula above enables you to expand this Static Degrees table to any extent desired.

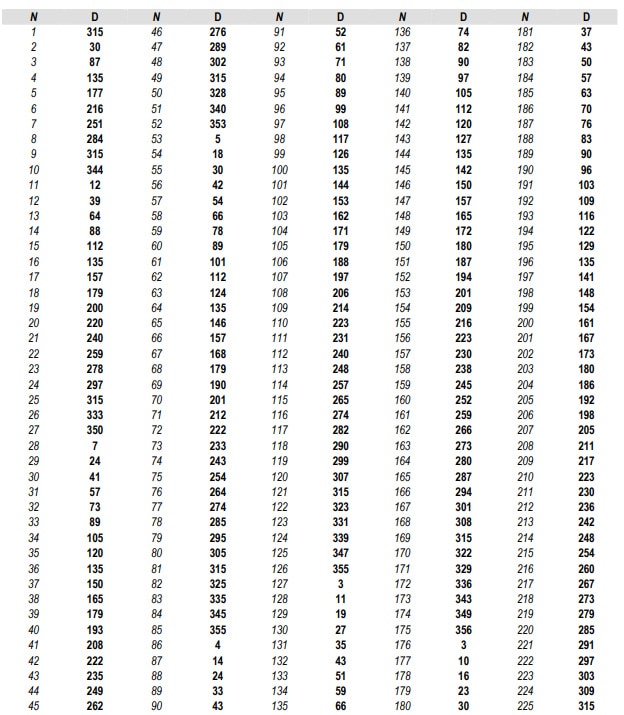
The degrees of a circle for the static numbers never change. The number 152 will always be on the 194 degrees angle, for example, and the number 9 will always be on the 315 degrees angle when applying the formulae, whether it’s a trading range of 9 points, 9 calendar days, or the closing price on any bar.

“For quick reference, use our online Square of Nine Calculator. “

For most of the applications going forward we will not be working directly in prices or days or bars but with the degrees of the circle that each of those items represents. As we now know the number of degrees will always be between 1 and 360, one complete rotation of the circle or the sum of the angles of a square.

So far as we know, this formula for converting price and time to degrees is attributable to Carl Futia and has been previously published or otherwise made generally available without any reservations. There are other formulae for determining angles, but this particular method is the least complicated, and it can be implemented easily on a cheap calculator or in a spreadsheet.

The purpose of the MOD 360 function is to manipulate the result to a number between 1 and 360. In our example above, we wanted to convert the intermediate result 1323.42. We could have done it this way. 3 x 360 = 1080 and 4 x 360 = 1440. The number 1323.42 is more than 3 x 360 and less than 4 x 360 so if we subtract out the 3 x 360 product (1323.42 – 1080 = 243.42) we are left with a desired number between 1 and 360.