The Gann Wheel
When presented with the idea of the Square of Nine, this illustration is most likely what you think of.

As with most things associated with Gann, they are described in colorful terms and made to look more difficult than they really are. The Gann Wheel or Square of Nine chart has been compared to or described as the floor plan of the Great Pyramid. Gann is said to have kept a scale model of the Great Pyramid with the peak labeled with the numeral one and each block consecutively numbered in a counterclockwise fashion.
You can easily imagine how this pyramid would be constructed, by grabbing the number one on the Gann Wheel and pulling it straight up to create a three dimensional object from the two-dimensional flat surface of the paper. This is probably a fairly useful thought experiment because it creates a clear picture in the mind of opposing sides, distinct angles, and the increasing distance between numbers, what we relate to as volatility, as you move further away from the numeral one on the top of the pyramid.
That the Great Pyramid of Gizeh also features prominently in the work of R.N. Elliott and the adherence of Fibonacci ratios to something built thousands of years ago is probably more than coincidental. For example, the Great Pyramid is 5,813 inches high (5-8-13) and the inch was the standard unit of measure in ancient Egypt. The ratio of the elevation to the base is .618. The total of the four edges of the base, measured in inches, is 36,524.22 which is exactly 100 times the length of the solar year. What does it all mean, who knows? In a totally unscientific affirmation it does suggest that the human brain may be hard-wired to respond in a certain way to very specific mathematical ratios and spatial relationships.
The Real Square of Nine?
Gann gave many courses on different aspects of his method but he never gave a course exclusively on the Square of Nine. We understand from others who have studied much of Gann’s original work that in one of his courses he did write about what he called a square of nine that looked something like this:

And although he never referred to it by any particular name, Gann also produced his own illustration of the Gann Wheel, what we call today the Square of Nine that is the same as the illustration on the website. We know that Gann used what we call the Gann Wheel to trade along with the complete version of the above table of 81 numbers as well as several other tables of numbers and geometric charts. Today we take for granted things like hand-held computers and wireless communications. In Gann’s day, you had to be a lot more creative and resourceful.
Use the Gann Wheel Then Put It Away
Although we will cover in this section a classic and simple use of the Gann Wheel to forecast price support and resistance levels, at the end of this section we will put the paper copy of the Gann Wheel away. The purpose of this short exercise is to provide a conceptual framework to the mathematical applications of the Square of Nine that is the heart of this work and much of Gann’s work as well. Later on it will be much easier to make sense of an expression like “19 is on the 90 degree angle” after you’ve seen how that works in two dimensions on the Gann Wheel.
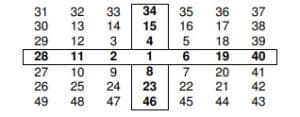
If you draw or imagine a circle around the outer edge of the above table, we can conceptualize the table as a rectangle inside a circle with a 360-degree circumference. The vertical line from 34 to 46 is at 0-180 degrees, and the left to right horizontal line from 28 to 40 on the table is at 270-90 degrees. In the example above, we can say that 19 is 90 degrees up from 15. The numeral 23 is 180 degrees up from 15 and 90 degrees up from 19. The numeral 8 would be 180 degrees down from 15. The “up” and “down” references mean greater or lesser numbers and not relative positions on the table. For example, 8 is 180 degrees down from 15, and 23 is 180 degrees up from 15, even though 8 and 23 are both on opposite sides of the horizontal 270-90 degree line.
In this very simple example we are using the Gann Wheel as a square root calculator. That may not be obvious to you at this point but when we start to do the math it will be. The number 15 lies conveniently on the 0-180 degree angle so it’s easy enough to show a 90 degree or 180 degree rotation. What if the number is not one of those on the most convenient fixed angles, say 37 on our small chart, which lies in the upper right hand corner? Most commercial Gann Wheels come with an acetate overlay with several angles printed on it. To calculate targets from 37 you would move the overlay to the right so that the zero or 360 degree angle lay on 37 and then read the angles of interest directly from the repositioned overlay.
We neither encourage nor discourage using a two-dimensional (paper) version of this square root calculator. After all people have been successfully using this tool for long before there was a Wall Street in New York or even a New World to put a New York in. Just be prepared for a steep learning curve. The paper version increments in whole numbers and can be difficult to apply to stock prices less than $150 and to many futures prices, which may require a radical conversion of one kind or another.
Of course, the folks who know these conversion factors aren’t going to tell you about them without serious cash changing hands, if at all. That being said, any number of books, courses, and seminars on applying the paper version of the Gann Wheel or the Square of Nine are available online or in person, and some have been available for many years. We haven’t traveled this road because we believe that there is an easier way.
| <<Back to Square of Nine Explained | Go to Square Root Theory |



Pingback: Mystery of W.D. Gann Square of Nine Explained 1.1 - Tradingfives.com
Pingback: Mystery Of W.D. Gann Square Of Nine Explained 3.1 - Circles Within The Wheel
Pingback: Mystery Of W.D. Gann Square Of Nine Explained 2.1 - Square Root Theory