Mystery of W.D. Gann Square of Nine Explained 3.1 – Circles Within the Wheel

The first practical application of the Square of Nine will make use of the degrees of the circle concept we developed with the Gann Wheel, a calculator, a pencil and an expanded Square Root Theory. We are expanding the Square Root Theory by adding divisions of whole numbers, and not just whole numbers, to the mix, and by moving beyond only price calculations to include a simple time element on the charts we will construct shortly.

Circles Within the Wheel

In the Gann Wheel section we said things like “19 is 90 degrees up from 15.” An expression like that makes sense only if we visualize a rectangular table of numbers enclosed in a circle of 360 degrees. It’s imperative to embrace the terminology because expressions like degrees and angles from here to there, or such and such price squaring with time on the 108 degree line are the lingua franca of the Square of Nine and essential to understanding how the different pieces fit together.

Time for more visualization. Using the number 15 on the above illustration as the focus, we can visualize a circle with the number 15 on its perimeter at a starting point of zero degrees. 19 is at 90 degrees, 23 is at 180 degrees, and 28 is at 270 degrees. The number 34 is directly above the number 15 and is positioned one ring outside the “circle.” Its position on the Square of Nine directly above 15 means that 34 is 360 degrees up from 15, or one complete rotation or cycle from 15. (28 is also outside the gray highlighted area but is not a rotation outside the “circle” because its position has not yet completed 360 degrees or one full  rotation from 15.)

Hopefully, circles within the wheel or the square within the circle visualization haven’t created any confusion. We did this illustration so that we could put some visual perspective on the math that accomplishes the same thing as one 360-degree rotation on the Square of Nine.

The square root of 15 is 3.87. Adding the number 2 to the square root of 15 results in 5.87. (3.87 + 2). That result squared is 34.49. We can immediately learn two things from this exercise: One is that the whole numbers on the Square of Nine ignore decimals and will inherently create rounding errors, and the second is that adding 2 to the square root of a number and squaring the sum is the same thing as a 360-degree rotation up on the Square of Nine. Subtracting the number 2 from the square root of 15 and then squaring the difference would be the equivalent of a 360-degree rotation down on the Square of Nine.

The Degrees to Factor Table

Now that you have the knowledge that a 360 degree move is the same as adding (or subtracting) 2 to the square root and then squaring the resulting sum or difference, we can expand this knowledge to produce the following:

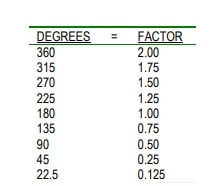
Degrees to Factor Conversion Table

The factor is the whole or decimal number that is added to or subtracted from the square root of the base number before squaring the result to move up, down or around on the Square of Nine. This simple table is Core Knowledge. Factors not shown on the Table can be derived easily. The factor for 67.5 degrees, for example, is .25 + .125 = .375. For most stock market work the major factors are those for 45 degrees and the multiples of 45 degrees.

Moving Around the Square of Nine

What number is 180 degrees up from 15? The answer is 23.75. The formula is (N ^.5 + factor) ^2, where N=15, the base number, and factor = 1 as determined from the Degrees-to-Factor table. Raising a number to the power of .5 or 1/2 is the same as solving for the square root. This is handy if your calculator has a power function key and does not have a square root function key. 90 degrees divides the circle into quarters, 45 degrees divides the circle into eighths, and 22.5 degrees divides the circle into sixteenths. You will find many cases where these divisions provide resistance and support from major and minor pivot points in every time frame.